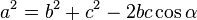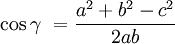Dalam kehidupan sehari-hari, sering kali kita di hadapkan pada suatu keadaan yang mengharuskan kita untuk membuat suatu keputusan. Agar keputusan kita itu baik dan benar, maka terlebih dahulu kita harus dapat menarik kesimpulan-kesimpulan dari keadaan yang kita hadapi itu, dan untuk dapat menarik kesimpulan yang tepat diperlukan kemampuan menalar yang baik.
Kemampuan menalar adalah kemampuan untuk menarik kesimpulan yang tepat dari bukti-bukti yang ada dan menurut aturan-aturan tertentu. Lalu apa kaitannya dengan logika?
Logika adalah ilmu untuk berpikir dan menalar dengan benar. Secara bahasa, logika berasal dari kata “logos” (bahasa Yunani), yang artinya kata, ucapan, pikiran. Kemudian pengertian itu berkembang menjadi ilmu pengetahuan. Logika dalam pengertian ini adalah berkaitan dengan argumen-argumen, yang mempelajari metode-metode dan prinsip-prinsip untuk ,menunjukkan keabsahan (sah atau tidaknya) suatu argumen, khususnya yang dikembangkan melalui penggunaan metode-metode matematika dan simbol-simbol matematika dengan tujuan untuk menghindari makna ganda dari bahasa yang biasa kita gunakan sehari-hari.
Nah sekarang, apa yang dimaksud dengan logika matematika???
Untuk lebih jelas klik : Logika Matematika
Source : Logika Matematika


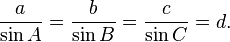

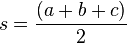

 adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut
adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut